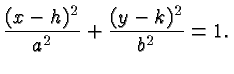WPP #12: Unit O Concept 10: Angles of Elevation and Depression

Steven is playing football and is given the chance to kick the ball into a the field goal.


He is at the 20 yd line and is getting ready to kick it up the 15 yd post. When he kicks it, it hits it exactly at the post. At what angle does he have to kick it to be able to hit the post?

When the ball comes back off the pole it falls 15 yds down and lands on the 30 yd line. At what angle is the ball coming at to the floor?

BQ#7: Unit V Concept 1: The Difference Quotients

When you are given a secant line on a graph with ONE point , you can find the other point by using the difference quotients...
How do you find the difference quotients?
Simple!
First look at the function.

When we give this function a point it will look like this 

We don't know exact numbers so we will give the x value x and the y value f(x) because it is a function. As you can see this is the point for the first point of the secant line. We need to be able to find the slope for this line in order to move on with anything else.

We need to know the point on the graph to be able to use this formula. We can get the other ordered pair on the graph by adding in another variable.

H stands for the length that we are missing. We use H to show that x has changed. When we write the next x value it will look like this...

We have to add x+h because that shows that we are adding both segments. The second point isn't just H. It is both x and h combined together and that is why we add them. The same thing for the y value. Now that we have our points, we are able to plug it in the slope formula. 

Next we are able to cancel variables like x's at the bottom

As a result, we have our difference quotients. Taking the derivative of the quotients formula will get you the slope from the secant line. 

f'(x)=2x will be the slope. From here you can use y=mx+b the find the tangent to any point on the function.

BQ# 6: Unit U Concept 1-8: Defining Limits

1. Continuity is when a function can be drawn without lifting your pencil from the paper. A continuous function also has no breaks, jumps, or holes.

 

 Although there is a hole in the function, the limit is there. A limit is an intended height, and this function is continuing on going through that intended height. The function is continuing on with it's pattern. The function is continuous. 

A discontinuity is a point in which the function stops and has a change in behavior. A jump discontinuity is when the function from the left and the right meet but have different y values, it changes and so you see two different segments. An infinite discontinuity is when there is a vertical asmyptote which leads to unbounded behavior and this causes the function to be discontinuous. An oscillating discontinuity with when the function has a very wiggly behavior and is very inconsistent, this means there is no definite point so the limit does no exist which means it is a discontinuity. 

2. A limit is the intended height in a function. A limit will always exist unless there is a jump discontinuity or infinite discontinuity or an oscillating graph. Besides these few points, their should be a limit at every single point you are on. If you happen to land on one of these points, the limit will not exist. The differences between a limit and a value is that a limit is the INTENDED height and the value is the ACTUAL height of the function.

3. When we evaluate a function numerically, we take a look at the table. We use tables to identify discontinuities. Evaluating a function graphically is the easier way you can look for limits/discontinuities. You can just take you fingers and bring them together to see what's going on on the graph. You will be able to see right away whether it is continuous or if there is a discontinuity. There are several steps in which you would have to do in order to evaluate a limit algebraically. You must first do substitution. You will substitute in the limit it is asking for and if you have a regular fraction or 0/#  or #/0 than that will be your limit. If it is 0/0 than it is indeterminate and you have to continue on by either factoring the equation or rationalizing/conjugate. From there you have to cancel out to remove the hole in the equation. Once things have canceled then you are able to use substitution again to find the limit, and that's how you evaluate a limit algebraically.

BQ#4: Unit T: Concept 3

In the Unit Circle, tangent and cotangent are both positive in the first quadrant and negative in the second. Then it is positive in the third and then negative in the fourth quadrant. The identity for tangent is tan(x)=sin(x)/cos(x) and the identity for cotangent is cot(x)= cos(x)/sin(x). This causes the asmyptotes to be place in different positions. The asymptotes for tangent are in different places than the asmyptotes for cotangent and this is what makes the trig graph go uphill or downhill.

The reason why tangent is going uphill and it is normal is because the first asymptote is place at pi/2 which is the end of the first quadrant. In the first quadrant the function needs to be going up, in order to go on to the next part of the function it needs to start down without touching the asymptote. That is why it starts over and starts down then goes up this is why it is going uphill.

Cotangent is different. The first asymptote  is mark at pi. This means the function can start up in quadrant one and progress down to quadrant two. There is no need for a new function to start because there is no asymptote separating those two quadrants. This is why it is normal for the function to be going down hill.

BQ#3: Unit T: Concepts 1-3

Sine and cosine are a part of every graph. When we go back to our identities we know that
a. tan(x)=sin(x)/cos(x)
b. cot(x)=cos(x)/sin(x)
c. sec(x)=1/cos(x)
d. csc(x)=1/sin(x)

Asymptotes from sine and cosine cause these graphs to differ. Sine and cosine are the only functions without a x or y in its denominator. All other trig functions do. Whenever sine (y) is 0 there will be an asymptote and that is where cotangent and cosecant have their asmyptote. The same goes for cosine (x), whenever it is 0 there will be an asymptote. This is what causes the trig graphs to change and differ.

BQ#5: Unit T Concepts 1-3

Whenever you have 0 in your denominator it will be undefined. You can only have an asymptote if you have an undefined number. All the trig functions have a ratio:

Sine               Cosine                  Cosecant                   Secant                  Tangent                Cotangent

      y/r                    x/r                           r/y                           r/x                         y/x                         x/y

When we are talking about the Unit Circle "r" matter what it equal to 1. When we look at the ratios, sine and cosine are the only trig functions where r is the denominator. This means no matter what the numerator is, the function will never be undefined because the denominator will always be 1. All the other functions have the possibility of being undefined because x or y can equal to 1 or 0 and that all depends on what point on the graph you are on. If you are on 0 or 180 or 360 degrees, cosecant and cotangent will be 0 because the ordered pairs on that point are (1,0) and 0 is y. If you are on 90 or 270 degrees, secant and tangent will be 0 because the ordered pairs are (0,1) and x is 0. 

BQ#2: Unit T Intro

1. The Unit Circle is a trig graph unraveled. It follows the same patterens as it does on the Unit Circle. When you have sine on the Unit Circle, it is going to be + + - -, on the trig graph it is the same thing it is up up then goes down down and that ends that period of the graph and on the Unit Circle it marks then end of a whole circle.

The period of sine and consine is 2pi because then you look at the negatives and positive from the Unit Circle, it takes one whole circle for the pattern of positives and negatives to start again. When you go around the Unit Circle completely that is 2 pi, that is why the period is 2pi. The reason why tangent and cotangent is pi is because it takes half the circle for the pattern to start over.

Sine and cosine are the only ones that have an amplitude, they are also the only two graphs that do not have that do not have asymptotes. All the other graphs have asymptotes because they certrain points where the graph is undefined and does not touch those points. With sine and cosine they graph will touch any points as long as they are within the amplitude. With all the other trig functions they have asymptotes. Amplitude and asymptotes are restrictions for each graph.

Reflection #1: Unit Q-Verifying Trig Identities

1. To verify a trig function is to show that the function given on the left side matches up the function given on the right side by simplify, substituting, and multiplying. You never touch the right side. The point is to get both sides to equal each other.

2. What has really helped me solve these functions was to memorizes all the identities. At first I thought it was pointless but when you are in the process of verifying or simplifying a trig function its a hassle to constantly having look back and forth. MEMORIZE! MEMORIZE! MEMORIZE!

3. The first thing I always do is try to change everything to sine and cosine. It makes everything a lot easier when it is in sine and cosine. Then I look for GCF. From there I look to cancel out anything and or combine like terms. From there I see if i can substitute an identity again and I'm usually done by this point.

I/D#3: Unit Q - Pythagorean Identities Concept 1: Using fundamental identities to simplify and verify expression (simple, one or two step identities)

1. When you draw a triangle inside a Unit Circle we use Pythagorean Theorem to finding the missing sides. We can use the Pythagorean Theorem to show why it is an identity.

It is referred to a Pythagorean Identity because you are using the Pythagorean Theorem to solve for the triangle and we have our ratios at the end of the equations which show that it is sine and cosine.  

Now if you were to plug in any of the coordinate points from the 30 45 60 degrees reference angles, you will always get answer that is equal to 1. For example:

2. To get the second identity from the Pythagorean Identities you have to take what you got from the first identity which was sin^2x+cos^2x=1 and divide it all by cos^2x. From there you use your ratio and reciprocal identities to find what each divided problem is equal to. And from there you have your tangent and secant identity.

To get the third identity you once again take your first Pythagorean Identity which was sin^2x+cos^2x=1 and divide it all by sin^2x. You then have to multiple divided identities and you use your ratio and reciprocal identities to find what each one equals too and from there you have your final identity that uses cotangent and cosecant

SP#7: Unit Q Concept 2: Find all trig functions when given one trig function and quadrant (Using identities)

This SP#7 was made in collaboration with Stephanie Vargas.  Please visit the other awesome posts on their blog by going here.

    You can solve this specific problem several different ways and this is one of them. In this SP we show you how to solve using identities and also using SOHCAHTOA. Make sure that you read all the side notes so you are able to understand what is going on and why we do each step. Solving using identities is trickier so make sure you look over each step as it is being done and refer back to you identities to understand why each step is happening.

BQ#1: Unit P Concept 2 & 3: Law of sines SSA (one, none, two solutions). Law of Cosines SSS or SAS

2. Law of Sines

The triangle always has to be able to fit in a scale of 180 degrees. With the given sides and angle you have to determine whether it will be two, one, or none answer(s). When you are finding the prime sides/angles you will have to use the very first angle that you have found in order to do so. You use the reference angle from the first answer to find the prime answers, the prime answer will be in quadrant II. If all your angles add up to more than 180 on your prime side, you will have no second answer. If BOTH your answers are more than 180, you will have NO answers. If both answers add up to 180 exactly, you will have TWO possible answers.

4. Area formulas

         This will work with any side you have. The height has created a right triangle and this let's you use trig-functions. The height will be whatever you get for the sine of C times the side of a. 

WPP#13&14: Unit P Concept 6-7: Applications with Law of Sines and Cosines

WPP#13-14 was made in collaboration with Stephanie Vargas. Please visit the other fantastic posts on their blog by going here.

I/D# 1: Unit N Concept 7 : Knowing All Degrees and Radians Around the Unit Circle, Knowing All the Ordered Pairs Around the Unit Circle, Understanding and Applying ASTC to the Unit Circle

30 Degrees Triangle 

45 Degrees Triangle 

60 Degrees Triangle & The Unit Circle

The coolest thing I learned from this activity was… the special right triangles that we learned about in geometry (which was way back in freshmen year) is actually related to the Unit Circles we began learning about sophomore year. I now know that the ordered pairs aren't just numbers put together randomly, I understand where these numbers come from.
This activity will help me in this unit because…I understand where these numbers come from when it comes down to labeling all ordered pairs. I am able to figure out how to get these ordered pairs if I ever forget what goes where. I can just draw my triangles and solve them to find my ordered pairs.
Something I never realized before about special right triangles and the unit circle is…that they are related. When I first started learning about special right triangles I thought it was going to be something that we just learned and weren't going to go back on it and use it later on like we do when we learned algebra. We are actually taking what we learned about special right triangles in geometry and finding the ordered pairs of them for the Unit Circles we are now learning about in Math Analysis (Pre-Calculus).

RWA #5: Unit M Concept 5: Graphing ellipse given equations (must complete the square first) and identifying all parts (center, focus, major axis, minor axis, vertices, co-vertices, eccentricity)

1. Ellipse- The set of all points such that the sum of the distance of the two points is a constant


2. Equation


Graph
https://www.youtube.com/watch?v=lvAYFUIEpFI

3. RWA- "'The Whisper Chamber' at the United States capital is another example of an ellipse's special properties. Stand at one focus and you can hear perfectly someone whispering at the other focus, though it is much too far away to hear if not for the reflective property specific to ellipses." The National Statuary Hall is were the US House of Representatives use to meet. You are able to whisper from the focus point of the room and the other person on the other focus point is able to here. 
4. References

• http://www.lessonpaths.com/learn/i/unit-m-conic-section-applets/ellipse-drawn-from-definition-geogebra-dynamic-worksheet
• http://www.math.utah.edu/online/1010/conics/
• https://www.youtube.com/watch?v=lvAYFUIEpFI
• https://sites.google.com/site/arinsellipse/real-life-examples